北航计算机学院 研究生 算法考试复习资料

不用再找了，这就是全网最全的北航算法复习资料

判断题

1. 贪婪技术所做的每一步选择所产生的部分解，不一定是可行性的

   ❌ 贪婪技术的核心：所做的每一步选择都必须满足：(1) 可行的，即它必须满足问题的约束； (2) 局部最优，即它是当前步骤中所有可行性选择中最佳的局部选择；(2) 不可取消，即一旦做出，在算法的后续步骤就无法改变了。

2. 一个正确的算法，对于每一个合法输入，都会在有限时间内输出一个满足要求的结。

   ✅

3. 动态规划中，各阶段所确定的策略就构成一个策略序列，通常称为一个决策

   ❌ 决策和策略：决策是指某阶段状态给定以后，从该状态演变到下一个阶段某状态的选择；由每段的决策组成的决策函数序列就称为全过程策略，简称策略。

4. 通常来说，算法的最坏情况的时间复杂性比平均情况的时间复杂性容易计算

   ✅

5. 回溯法用深度优先法搜索状态空间树

   ✅ 针对所要做的选择构造一棵所谓的状态空间树，树的每一层节点代表了对解的每一个分量所做的选择；用DFS（深度优先法）搜索状态空间树；在状态空间树中的任一个节点，满足一定条件的情况下，搜索回溯。

6. 快排算法的平均时间复杂度是 O(nlogn), 使用随机化快排算法可以将平均时间复杂度降得更低

   ❌ 平均时间复杂度不会降低，只会降低最坏情况出现的概率。最坏情况出现在随机数生成结果恰好使数组有序----概率极小。

7. P 类问题和 NP 类问题的关系用 $p\subset NP$ 来表示是错误的

   ❌ P 中所有问题都属于 NP

   

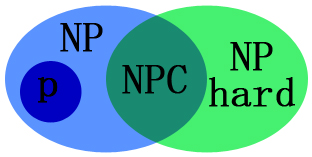
8. NP 完全问题比其他所有 NP 问题都要难

   ❌ NP 完全问题至少同其他所有 NP 问题一样难，NP-hard 问题：比 NP 问题都要难的问题

   https://zhuanlan.zhihu.com/p/73953567

   • P类问题：存在多项式时间算法的问题。(P：polynominal，多项式)。

   • NP问题：能在多项式时间内验证得出一个正确解的问题。(NP:Nondeterministic polynominal，非确定性多项式)。

   • NPC类问题（Nondeterminism Polynomial complete）：存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。其定义要满足2个条件：

     • 首先，它得是一个NP问题；
     • 所有的NP问题都可以约化到它。
     • 要证明npc问题的思路就是： 先证明它至少是一个NP问题，再证明其中一个已知的NPC问题能约化到它。

   • NP难问题（NP-hard问题）：

     NP-Hard问题是这样一种问题，它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比 NPC问题的范围广，NP-Hard问题没有限定属于NP），即所有的NP问题都能约化到它，但是它不一定是一个NP问题。

9. 若 P2 多项式时间转化为 P1，则 P2至少与 P1 一样难

   ❌ P2 不会比 P1 难，P1 至少与 P2 一样难。

10. 一个完全多项式近似方案是一个近似方案 {A, } 其中每一个算法 A，在输入实例 I 的规模的多项式时间内运行。

    ❌ 一个多项式近似方案(PAS)是一个近似方案{AƐ},其中每一个算法AƐ 在输入实例I的规模的多项式时间内运行;一个完全多项式近似方案(FPAS)是一个近似方案{AƐ},其中每个算法 AƐ在以输入实例的规模和1/Ɛ两者的多项式时间内运行

    http://home.ustc.edu.cn/~huang83/turing/alg5.pdf

    • 近似方案：设$\pi$是目标函数为݂$f_\pi$的NP-hard最优化问题，如果关于输入$(I,\varepsilon)$，$I$ 为$\pi$的实例，$\varepsilon$ 为误差参数，算法$A$输出解ܵ使得：（最小化问题）$f_\pi(I,S)\le(1+\varepsilon)*OPT$ 称$A$ 是 $\pi$ 的近似方案
    • PTAS (Polynomial-Time Approximation Scheme ) 若对于每一个固定的$\varepsilon$，算法的运行时间以实例$I$的规模的多项 式为上界，则$A$是一个多项式时间近似方案(简称PTAS)。
    • FPTAS 在PTAS的基础上，我们进一步要求算法，即算法A的运行时间以 实例$I$的规模和$1/\varepsilon$ 的多项式为上界，则称$A$是一个完全多项式时间近似方案(简称FPTAS)。近似算法的复杂度和精度要求有关

11. 基于比较的寻找数组 A[1...n] 中最大值元素问题的下界是 $\Omega(n/3)$

    ❌ 只寻找最大值，下界是 O(n-1) ，同时寻找最大值和最小值，下界是 $O(3n/2)$，

    首先两两比较，分成A组与a组，每组n个，此时用了n次。A组内取最大，用n-1次，a取最小也是n-1次。一共n+(n-1)*2

12. Las Vegas 算法只要给出解就是正确的

    ✅ Las Vegas 算法总是要么给出正确的解，要么告知无解

    拉斯维加斯算法 (Las Vegas) 是另一种随机算法，因此它具备随机算法最为重要的特征之一 —— 基于随机数进行求解。与 蒙特卡洛算法 (Monte Carlo) (opens new window) 一样，拉斯维加斯算法也不是一种具体的算法，而是一种思想。但不同的是，拉斯维加斯算法在生成随机值的环节中，会不断的进行尝试，直到生成的随机值令自己满意。在这过程中也许会一直无法产生这样的随机值，因此拉斯维加斯算法的时间效率通常比蒙特卡洛算法来的低，并且最终可能无法得到问题的解，但是一旦算法找到一个解，那么这个解一定是问题的正确解。

    **拉斯维加斯算法不赌结果的正确性，而是赌运算所用资源。**一个简单的例子是随机快速排序 (opens new window)，他的中心点虽然是随机选择的，但排序结果永远一致。

13. 若近似算法 A 求解某极小化问题一实例的解为 $s_a$ ，且已知该问题的最优解为 $s_a/3$ 则该近似算法的性能比为 3

    ❌ 不能只看某一实例的解，应该要寻找问题所有实例的上界

14. $O(f(n))+O(g(n)) = O(min\{f(n), g(n)\})$

    ❌ $O(f(n))+O(g(n)) = O(max\{f(n), g(n)\})$

15. $\Theta(f(n)+g(n)) = \Theta (max(f(n),g(n)))$

    ✅

16. 若 $f(n)=\Omega(g(n))$, $g(n) = \Omega(h(n))$ 则 $f(n)=\Omega(h(n))$

    ✅

$\begin{array}{l} O(f(n))+O(g(n))=O(\max \{f(n), g(n)\}) \\ O(f(n))+O(g(n))=O(f(n)+g(n)) \cdot \\ O(f(n))^{*} O(g(n))=O\left(f(n)^{*} g(n)\right) \\ O(c f(n))=O(f(n)) \\ f(n)=O(g(n)), \quad g(n)=O (h(n)) \Rightarrow f(n)=O (h(n)) \\ f(n)=\Omega(g(n)), \quad g(n)=\Omega(h(n)) \Rightarrow f(n)=\Omega(h(n)) ; \\ f(n)=\Theta(g(n)), \quad g(n)=\Theta(h(n)) \Rightarrow f(n)=\Theta(h(n)) ; \end{array}$

$\begin{array}{l} f(n)=\Theta(g(n)) \Leftrightarrow g(n)=\Theta (f(n)) \\ f(n)=O(g(n)) \Leftrightarrow g(n)=\Omega(f(n)) \\ f(n)=\Theta(f(n)) \\ f(n)=O(f(n)) \\ f(n)=\Omega(f(n)) \end{array}$

17. 若$f(n)=O(g(n))$, 则 $g(n)=\Omega(f(n))$

    ✅ Ο是渐进上界，Ω是渐进下界。Θ需同时满足大Ο和Ω，故称为确界（必须同时符合上界和下界）。

18. NP 完备（NP-Complete）问题是所有 NP 问题中最难的，目前还没 有找到用于解决 NP 完备问题的多项式算法。

    ❌

19. 已知团问题（Clique problem）为NP问题，那么下列问题是一个判定问题：给定一个图G，求G中最大团的尺寸（size）K。

    ❌

20. 随机化快速排序的worst case 出现于输入数组恰好为已按非降序排列的情况（假设输出的排序结果也要求是非降序）。

    ❌

21. 动态规划算法通过增加空间复杂性来降低时间复杂性。

    ✅

22. 回溯法用深度优先或广度优先法搜索状态空间树。

    ❌

23. 若求解问题p的一个算法A的复杂性为f(n) ，则p的复杂性C(p)小于等于f(n)。

    ✅

24. 所有问题当中最难的一组问题被称为NP完备 (NP-Complete) 问题。

    ❌

简答题

1. 二叉查找树属于减治策略的三个变种中哪一个的应用？什么情况下二叉查找树表现出最差的效率？此时的查找和插入算法的复杂性如何？

   1. 二叉查找树属于减可变规模变种的应用

      减治策略的三个变种： 减常量、减常数因子、减可变规模

      • 减去一个常量(a constant) DFS，BFS
      • 减去一个常数因子(a constant factor) 折半查找
      • 减去的规模是可变的(variable size desrease) 二分查找

   2. 表现出最差的效率：当先后插入的关键字有序时，构成的二叉树变为单枝树，树的深度为 n ，此时二叉查找树表现出最差的效率

   3. 此时查找和插入算法的时间复杂度都为 O(n)

2. 构造 AVL 树和 2-3 树的主要目的是什么？他们各自有什么样的查找和插入的效率

   1. 主要目的：一棵AVL树要求它的每个节点的左右子树的高度差不能超过1。2-3树和2-3-4树允许一棵查找树的单个节点不止包含一个元素。构造 AVL 树和 2-3 树，可以使先后插入的关键字有序时，使树的深度减少
   2. 查找和插入效率：AVL 树，插入和查找效率为 O(logn)，2-3 树的查找和插入效率属于 O(logn)

3. 写出 01 背包的一个多项式等价的判定问题，并说明为什么他们是多项式等价的

   0/1背包问题：从M件物品中，取出若干件放在空间为W的背包里，给出一个能获得最大价值的方案。每件物品的体积为W1，W2……Wn，与之相对应的价值为P1,P2……Pn。

   • 判定问题I：从M件物品中，取出若干件放在空间为W的背包里，是否存在一个方案，所获价值≥P*？。每件物品的体积为W1，W2……Wn，与之相对应的价值为P1,P2……Pn。
   • 对于判定问题P，以及输入N, w, v, W, V：构造对应的背包问题P0，求出P的最大价值和V0，与问题P的输入V进行比较即可判定是否存在，即 P 规约到 P0 对于背包问题 P0，在0和所有元素的价值总和Vmax之间进行二分，每次构造判定问题P，即可求得P0的解。即 P0 规约到 P。因此他们是多项式等价的

4. 何谓伪多项式算法？如何将一 Monte Carlo 算法转化为 Las Vegas 算法

   • 伪多项式时间算法是一种算法，它在 L 值的多项式时间内运行，其中 L 是输入实例中的最大数值

     算法的复杂度与输入规模呈指数关系，与输入的数值大小呈多项式关系。

   • Las Vegas算法不会得到不正确的解。一旦用拉斯维加斯算法找到一个解，这个解就一定是正确解。但有时用拉斯维加斯算法找不到解。

     Monte Carlo算法每次都能得到问题的解，但不保证所得解的准确性

     转化：可以在Monte Carlo算法给出的解上加一个验证算法，如果正确就得到解，如果错误就不能生成问题的解，这样Monte Carlo算法便转化为了Las Vegas算法。

5. 以子集和问题为例说明伪多项式时间算法和FPAS可以有的关系。

   • 时间复杂度表示为输入数据数值规模N的多项式，但是运行时间却与N的二进制成指数关系，这样的时间复杂度的算法称为伪多项式时间的算法。
   • FPTAS 在PTAS的基础上，我们进一步要求算法，即算法A的运行时间以 实例$I$的规模和$1/\varepsilon$ 的多项式为上界，则称$A$是一个完全多项式时间近似方案(简称FPTAS)。近似算法的复杂度和精度要求有关
   • 为NP难问题找到一个FPAS的想法对存在伪多项式时间算法的问题来说是很典型的。可以对实例 I 的输入值应用尺度变换和舍入得到实例 I' 并解之
   • 对于子集和问题，算法的近似度是$1+\varepsilon$ ，运行时间是$\Theta (n^2/\varepsilon)$

6. 下面的问题是否属于 NP 问题？为什么？

   给定图 G=(N,A) 中的两个点 p、q，整数 c 和 t，图 G 中每条边的长度 cij 及便利这条边的时间 tij。问图 G 中是否存在一条由 p 到 q 的路径，使得其长度大于 C，且遍历时间小于 t？

   • 这个问题属于 NP 问题（多项式时间内验证解）。因为若给出该问题的一个解，可以在多项式时间内验证这个解的正确性。如给出一条由 p 到 q 的路径，可以在多项式时间内计算出它的长度和遍历这条路径的时间，然后分别于 C 和 t 进行比较，从而可以判断出这个解的对错

7. 请给出基于比较的对数组 A[1…n]进行排序问题的最紧的下界，并写出两个 平均时间复杂度为该下界的排序算法的名称。

   • 下界为 $O(nlogn)$
   • 快排，归并排序

8. 请举出三种寻找问题下界的方法或策略

   寻找下界的策略：

   • 平凡下界：对问题的输入中必须要处理的项及必须要输出的项进行计数
   • 信息量论证
   • 对手规约
   • 问题规约

9. 说一个有最优解的贪心算法？

   • 最短路径、Dijstra、哈夫曼编码

10. ​ 推导以下递推式的解：

    T(n)=2 当n=3时

    T(n)=2T(n/3)+2n 当n>3时

    

11. 求解TSP问题的最近邻居算法的性能比是多少？这一性能比是如何求得的？

    最近邻居算法：基于一种最近邻居的直观推断：下一次总是访问最近的未访问城市

    第一步：任意选择一个城市作为起点 第二步：重复下面的操作直到访问完所有的城市：访问和最近一次访问的城市 k 最接近的未访问城市（如 果有距离相同的城市，可任意选择其一） 第三步：回到起点城市

    性能比：

    $\frac{m\left(x, s_{a}\right)}{m *(x)} \leq \frac{1}{2}\left(\left\lceil\log _{2} n\right\rceil+1\right)$

    这一性能比是在欧几里得类型 TSP 问题约束下求得的

12. 请给出基于比较的寻找数组A[1…n]中最大和最小元素问题的最紧的下界，并说明这个下界是用了课上介绍的哪种或哪几种寻找问题下界的策略得来的。

    • 寻找下界的策略：

      • 平凡下界：对问题的输入中必须要处理的项及必须要输出的项进行计数
      • 信息量论证
      • 对手规约
      • 问题规约

    • 使用 3n/2-2次比较可计算最大值与最小值

      算法初始把所有元素标记为N，且算法运行过程中必须标 记n-1次W和n-1次L，因此至少需要2n-2 “信息单位” 。 每次比较中能得到的最大信息量为2，且只当比较两个标记为N的 元素时产生。但此种情况最多产生 n/2次，共n个信息单位 。 除此以外的其他比较最多产生1个信息量，因此对于剩下的n-2个 信息量，最坏情况下需要 n-2次比较。

    • 运用了对手规约的方法得来的

13. 请给出寻找数组A[1…n]中是否有大于0的元素问题的最紧的下界，并说明这个下界是用了课上介绍的哪种或哪几种寻找问题下界的策略得来的。

    下界是 n，使用平凡下界的策略得来

14. 是否存在具有最小绝对差界的求解地图着色问题的近似算法？若有，请写出伪代码，并说明为什么其绝对差界已达最小。

15. 

16. 用对手论证法给出最坏情况下，从n个数字中找第二小值的基于比较的算法的下界；这个下界是紧密的吗

    算法的下界是：$n+\lceil \log n \rceil -2$

    每次两两进行配对，利用淘汰赛求得最大值max（n-1次比较）；然后从所有与max进行比较输了的元素中找到最大值（log2n-1次 比较）

    这个下界是紧密的

17. 在最坏情况下，任意一个基于比较的算法从n个 元素（假设n为偶数）中确定最大值和最小值至少需要 (3n/2)-2 次比较。

    证明：算法初始把所有元素标记为N，且算法运行过程中必须标 记n-1次W和n-1次L，因此至少需要2n-2 “信息单位” 。 每次比较中能得到的最大信息量为2，且只当比较两个标记为N的 元素时产生。但此种情况最多产生 n/2次，共n个信息单位 。 除此以外的其他比较最多产生1个信息量，因此对于剩下的n-2个 信息量，最坏情况下需要 n-2次比较。 因此，最坏情况下，至少需要 n/2 + n-2 =3n/2 – 2次比较。

18. 请分别阐述邻域搜索、模拟退火与遗传算法的基本原理，并从算法特点与计算效果等角度比较它们的异同

    遗传算法：

    • 基本原理：遗传算法是一种基于群体寻优的方法， 算法运行是以一个种群在搜索空间进行搜索，根据具体问题构造恰当适值函数，根据适应值的大小不断选择和繁殖

    • 特点：

      • 同时处理群体中的多个个体，减少了陷入局部最优解的风险，算法本身易于并行化

    邻域搜索：

    • 基本原理：基于贪婪思想, 持续地在当前解的邻域中搜索, 直至 邻域中再也没有更好的解, 也称为爬山启发式算法
    • 特点：
      • 易理解易实现, 具有很好的通用性,
      • 但搜索结果完全依赖于初始解和邻域的结构 ，只能搜到局部最优

    模拟退火：

    • 模拟热力学中退火过程能使金属原子达到能量最低状态的 机制， 通过模拟的降温过程按波尔兹曼方程计算状态间的 转移概率来引导搜索，
    • 特点：
      • 具备良好的全局搜索能力，最终解逼近全局最优解，对初始解的依赖较低

19. 说明最小生成树的Prim算法不具有拟阵的结构，即说明Prim算法所对应的二元组 M=(S,I)不满足遗传性质或不满足交换性质。

    拟阵是一个满足如下条件的有序对：M=(S,I)

    • S 是非空有限集
    • I 是 S 子集的一个非空族，这些子集称为 S 的独立子集，I 满足遗传性质，若 $B \in I$, 且 $A \subseteq B$, 则 $A\in I$
      • 若 B 是 S 的独立子集，则 B 的任意子集均是 S 的独立子集
    • I 满足 交换性质，若 $A\in I$ , $B\in I$ 且 $|A|<|B|$ 则存在某个元素 $x\in B-A $ 使得 $A \cup \{x\} \in I$

    • 对于给定的无向图 G=(V,E) 定义$S_G$ 为图的边集 E
    • 由于Prim 算法的每一步，均生成 V 的子集的最小生成树， $I_G$ 是最小生成树边集的非空族，即 $I_G$ 中的每一个集合均构成 V 中部分顶点的最小生成树
    • $I_G$ 不满足遗传性质，最小生成树边集的子集不一定构成最小生成树，最小生成树边集的子集可能只是一个森林

20. 分支定界算法遍历搜索树的“Frontier Search”，是如何工作的？为什么会有这样一种方法？（本题 3 分）

    • 在构造二叉树时，将分支按照一定的规则进行排序，可以使得解树向左偏，即最优解更可能出现在左分支上。使得 Frontier Search 能够更早的寻找到最优解，提高剪枝效率。

编程题

变治法

1. 变治法解数列多数元素问题：

   • 思路：先排序，然后线性扫描。复杂度O(nlogn) + O(n) = O(nlogn)

   • 算法：

     sort(src);//对整数序列进行排序
     count = 0;
     num = src[0];
     temp = floor(n / 2)
     for( i = 0; i < n; i++)
     {
         if(num == src[i])
         {
             count ++;
             if(count > temp)
             {
                 cout << "Exist" << endl;
                 break;
             }
         }
         else
         {
             num = src[i];
             count = 1;
         }
     }
     if(i == n)
         cout << "Doesn't exist" << endl;
     

分治法

1. 变治法解数列多数元素问题：

   https://leetcode-cn.com/problems/majority-element/solution/duo-shu-yuan-su-by-leetcode-solution/

   • 思路：

     如果数 a 是数组 nums 的众数，如果我们将 nums 分成两部分，那么 a 必定是至少一部分的众数。

     我们可以使用反证法来证明这个结论。假设 a 既不是左半部分的众数，也不是右半部分的众数，那么 a 出现的次数少于 l / 2 + r / 2 次，其中 l 和 r 分别是左半部分和右半部分的长度。由于 l / 2 + r / 2 <= (l + r) / 2，说明 a 也不是数组 nums 的众数，因此出现了矛盾。所以这个结论是正确的。

     这样以来，我们就可以使用分治法解决这个问题：将数组分成左右两部分，分别求出左半部分的众数 a1 以及右半部分的众数 a2，随后在 a1 和 a2 中选出正确的众数。

   • 算法：

     我们使用经典的分治算法递归求解，直到所有的子问题都是长度为 1 的数组。长度为 1 的子数组中唯一的数显然是众数，直接返回即可。如果回溯后某区间的长度大于 1，我们必须将左右子区间的值合并。如果它们的众数相同，那么显然这一段区间的众数是它们相同的值。否则，我们需要比较两个众数在整个区间内出现的次数来决定该区间的众数。

     class Solution:
         def majorityElement(self, nums, lo=0, hi=None):
             def majority_element_rec(lo, hi):
                 # 递归终止条件，数组中仅有一个元素，众数就是他本身
                 if lo == hi:
                     return nums[lo]
     
                 # 二分，寻找两边的众数
                 mid = (hi-lo)//2 + lo
                 left = majority_element_rec(lo, mid)
                 right = majority_element_rec(mid+1, hi)
     
                 # 如果两边的众数相同，就返回其中一边
                 if left == right:
                     return left
     
                 # 否则，计算比较哪边的众数比较大
                 left_count = sum(1 for i in range(lo, hi+1) if nums[i] == left)
                 right_count = sum(1 for i in range(lo, hi+1) if nums[i] == right)
     
                 return left if left_count > right_count else right
     
             return majority_element_rec(0, len(nums)-1)
     
     

   • 复杂度

     时间复杂度：$O(n\log n)$。函数 majority_element_rec() 会求解 2 个长度为 $\dfrac{n}{2} $的子问题，并做两遍长度为 n 的线性扫描。因此，分治算法的时间复杂度可以表示为：

     $T(n) = 2T(\frac{n}{2}) + 2n$

     根据 主定理，本题满足第二种情况，所以时间复杂度可以表示为：

     $\begin{aligned} T(n) &= \Theta(n^{log_{b}a}\log n) \\ &= \Theta(n^{log_{2}2}\log n) \\ &= \Theta(n \log n) \\ \end{aligned}$

     空间复杂度：$O(\log n)$。尽管分治算法没有直接分配额外的数组空间，但在递归的过程中使用了额外的栈空间。算法每次将数组从中间分成两部分，所以数组长度变为 1 之前需要进行 $O(\log n)$次递归，即空间复杂度为 $O(\log n)$。

2. 分治算法解逆序元素对的数目

   • 思路：

     • 划分
       • 对一个序列划分为左右两个子序列（当划分到最后只剩下两个元素时便可直接判断），逆序对的有三种存在情况：1.在左子序列中；2.在右子序列中；3.由左右子序列共同构成。
       • 当划分到只剩下一个元素时，开始回溯合并
     • 求解：左右子序的元素顺序遍历比较大小（即归并排序的比较）
     • 合并：合并过程中左右子序均按升序排序，当出现左子序列元素值大于右子序列中的某个元素值时，此时左子序列中的该元素及其后面的所有元素，均可与右子序列中的这个元素构成逆序对

   • 算法：

     class Solution:
         def mergeSort(self, nums, tmp, l, r):
             if l >= r:
                 return 0
     
             mid = (l + r) // 2
             # 划分，计算左右两个子序列的各自逆序数
             inv_count = self.mergeSort(nums, tmp, l, mid) + self.mergeSort(nums, tmp, mid + 1, r)
             # 合并
             i, j, pos = l, mid + 1, l
             while i <= mid and j <= r: # 两个子序列依次从前往后遍历
                 if nums[i] > nums[j]: # 前半段出现了比 后半段大的元素
                     tmp[pos] = nums[i]
                     i += 1
                     inv_count += (j - (mid + 1)) # 这时，左序列中的该元素，及其后面的所有元素，均可与右序列中的这个元素构成逆序对
                 else:
                     tmp[pos] = nums[j] # 否则，正常排序
                     j += 1
                 pos += 1
             for k in range(i, mid + 1): # 右半段用完，这时，左半段剩余所有元素，都可以与右半段最后一个元素构成逆序对
                 tmp[pos] = nums[k]
                 inv_count += (j - (mid + 1))
                 pos += 1
             for k in range(j, r + 1): # 左半端用完，正常排序
                 tmp[pos] = nums[k]
                 pos += 1
             nums[l:r+1] = tmp[l:r+1]
             return inv_count
     
         def reversePairs(self, nums: List[int]) -> int:
             n = len(nums)
             tmp = [0] * n
             return self.mergeSort(nums, tmp, 0, n - 1)
     
     

   • 复杂度：

     记序列长度为 n。

     时间复杂度：同归并排序 O(nlogn)。 空间复杂度：同归并排序 O(n)，因为归并排序需要用到一个临时数组。

   • 与暴力解法比较：

     暴力解法：使用两层 for 循环枚举所有的数对，逐一判断是否构成逆序关系。时间复杂度：$O(n^2)$; 空间复杂度：O(1)。

3. 设计一求解以下问题的分治算法，写出伪代码，分析其时间复杂性并与该问题的蛮力算法相比较

   问题描述：设有 n=2 k 个运动员要进行网球循环赛。现要设计一个满足以下要求 的比赛日程表：

   ​ （1）每个选手必须与其他 n-1 个选手各赛一次；

   ​ （2）每个选手一天只能参赛一次；

   ​ （3）循环赛在 n-1 天内结束。

   请按此要求将比赛日程表设计成有 n 行和 n-1 列的一个表。在表中的第 i 行，第 j 列处填入第 i 个选手在第 j 天所遇到的选手。其中 1≤i≤n，1≤j≤n-1。

4. 设计一求解以下问题的分治算法，写出伪代码，分析其时间复杂性并与该问题的蛮力算法相比较：

   某投资咨询公司要长期重复做一项模拟，在这项模拟中他们从过去的某天开始对一支给定的股票连续考察n天（这些天数记为 i = 1,2,...n）；对每天i，有当天这只股票每股的价格p(i)（为简单起见，我们假设这个价格在每一天之内是固定的）。 假设在这n天内，某天买进这支股票并且在以后的某天卖出这些股票，欲求：为了挣到最多的钱，他们应该什么时候买进并且什么时候卖出？

   举例说，假设n=4，p(1)=4，p(2)=1，p(3)=1.5，p(4)=3，那么你的算法应该返回“2买，4卖”（在第2天买并且在第4天卖意味着每股将挣2美元，是这个期间最大的收益）。

减治法

写出一具有减治思想的求$log_2N$的算法，并推导其时间复杂性。

动态规划

1. 某工厂调查了解市场情况，估计在今后四个月内，市场对其产品的需求量如下表所示。（仓储问题？）

时期（月）	需要量（产品单位）
1	2
2	3
3	2
4	4

已知：对每个月来讲，生产一批产品的固定成本费为3 (千元)，若不生产，则为零。每生产单位产品的成本费为1 （千元)。同时，在任何一个月内，生产能力所允许的最大生产批量为不超过6个单位。

又知每单位产品的库存费用为每月0.5 （千元），同时要求在第一个月开始之初， 及在第四个月末，均无产品库存。

问：在满足上述条件下，该厂应如何安排各个时期的生产与库存，使所花的总成本费用最低？写出你所设的状态变量、决策变量、状态转移方程与递推关系式，和手工求解的详细步骤及结果。

• 状态变量：$x_k$ ：第 k 月初的存储量

• 决策变量：$u_k$ ：第 k 月的产量

• 状态转移方程：$x_{k+1} = x_k + u_k - s_k$

• 指标函数：$V_{k,n} = \sum_{j=k}^n v_j(x_j,u_j)$

  $v_k=0.5x_k+u_k + 3I_{u_k\neq1}(u_k)$

  允许决策集合：$D_k(x_k) = \{u_k| 0\le u_k \le 6, u_k + x_k - s_k > 0\}$

• 递推关系式：

  $\left\{\begin{array}{l} f_{5}\left(x_{5}\right)=0 \\ f_{k}\left(x_{k}\right)=\min _{u_{k} \in D_{k}\left(x_{k}\right)}\left\{0.5 x_{k}+u_k+3I_{u_k\ne1}(u_k)+f_{k+1}\left(x_{k+1}\right)\}\right. \end{array}\right.$

1. 

• 状态变量：剩余的投资金额：$x_k$

• 决策变量：为每个项目投资的数额：$u_k$

• 状态转移方程：$x_{k+1} = x_k-u_k$

• 指标函数：$V_{k,n} = \sum_{j=k}^n v_j(x_j,u_j)$

  $v_k=s[x_k] - x_k$

  允许决策集合：$D_k(x_k) = \{u_k|0\le u_k \le x_k\}$

• 递推关系式：

  $\left\{\begin{array}{l} f_4(x_4) = 0 \\ f_k(x_k) = \max_{u_k\in D_k(x_k)}\{ s[x_k] - x_k + f_{k+1} (x_{k+1}) \} \end{array}\right.$

1. 写出用动态规划方法求两个序列的最长公共子序列算法的递推 公式、伪代码和时间复杂性，并用该算法手工计算以下 X 和 Y 的最长公共子 序列：

   X=abcbcc，Y=cacbac

2. 设计一基于动态规划思想求解以下问题的算法，写出递推关系式、伪代码，并分析你所设计的算法的时间复杂性：

   一条公路由西到东长M公里，公路两旁可能设立广告牌的地点为 x ，而在各地点放置一块广告牌带来的收益分别 p。有关规定要求两块广告牌的距离不能小于3公里。要求找到一组地点来放置广告牌，使得总收益最大。

分支定界

某部门欲建立联通分布于五个区的共50个站点的有线通信网络。每两个站点之间的线路敷设费用由对称矩阵C给出。任意两站点之间敷设线路需建设的地井数目由对称矩阵U给出。

设计一线路敷设总费用为最小的无环网络，使得需建设的总地井数目不超过UMAX，且需跨区敷设的线路总数目不超过DMAX（各站点所属的区由向量D给出）。

1. 说明你是如何构造搜索树的。（要求是二叉搜索树）。
2. 说明算法遍历搜索树的原则（何时以及如何前进、分支、回溯、剪枝等等）。
3. 你设计的分支定界算法的“界”是什么，它为什么是正确的和有效的？
4. 写出伪代码。

• 50 个节点的原始网络为一个无向完全图，总的边数为 50*49/2 = 1225 条，因此，以边为节点构造一个 1225 层的二叉搜索树，对所有边按照铺设费用从小到大排序，编号为 1... 1225 。对于第 i 层的分支，对应于是否把第 i 条边添加到解集中，左分支代表选择该边，右分支表示不选择该边

• 遍历搜索树的原则

  • 前进：在当前层，选择最可能达到最优的结点进行扩展，要满足欲加入的边满足网络无环、以及地井和线路数的限制
  • 分支：左支表示将该边加入到解集，右支代表不将该边加入到解集
  • 回溯：当前挑选的边使解不可行，或已经找到一个解时回溯，当从左分支回溯会节点时，接着遍历右分支，从右分支回溯时，回到父节点
  • 剪枝：在搜索树的每个节点，进行可行性检查，并且计算下界，若当前节点不可行，或计算出的下界超过了当前已求出的最优解，则进行 剪枝
  • 停止：当二叉树所有节点都被访问过时，可以找到一个最优解

• 分支定界法的界：

  • 下界：不考虑限制条件，在当前已经敷设的线路的基础上，用修改的 Kruskal 算法，构造的最小生成树的总花费
  • 正确和有效的原因：加上任何约束条件的情况下，可行解的花费均大于等于最小生成树的费用代价

• 伪代码：

  def search(S, l):
  	if（ isNoCircle(S)
  			 && countU(S) <= UMAX
  			 && countD(S) <= DMAX
  			 && minBound(S) < bestSolutionNow) {
  			 	if (S 已经覆盖所有站点)
  			 		记录最优结果 BestS=S
  			 		更新 bestSolutionNow
  			 	else {
  			 		search(S+l, l->left)
  			 		search(S, l->right)
  			 	}
  			 }
  	
  
  BuildNetwork() {
  	Tree = buildTree() # 初始化，根据边集合，构造二叉搜索树
  	search(空集，Tree->root)
  	return BestS
  }
  

A国和B国之间尚未直接通商。但是，与A国直接通商的有20个国家(C1、C2、…C20)；与B国直接通商的为另外30个国家（C21、C22、…C50）。上述50个国家(C1、C2…C50)之间并不是每两个国家都直接通商，任意两国之间的贸易税率由对称矩阵R给出，其中“无穷大”代表两国之间不能直接通商。

​ A国某公司和B国某公司欲通过某几个中间国家的公司完成一笔贸易，各个国家的进出口贸易通关等程序所需办理时间由向量T给出。请安排一个中转贸易计划，使得该交易所产生的向各中转国缴纳的税费最低，且整个交易能够在时间t内完成。

1、 说明你是如何构造搜索树的（要求是二叉搜索树）

2、 说明算法遍历搜索树的原则（何时以及如何前进、分支、回溯、剪枝等等）

3、 你设计的分支定界算法的“界”是什么，他为什么是正确的和有效的？

4、 写出伪代码。

• 如何构造搜索树：根节点为 A 节点，每个节点的左分支表示其代表的国家为下一个贸易顺序上的国家，右分支表示该国家不加入贸易顺序。树的每一个节点由之前的贸易顺序 S，和已经否决的国家 V 构成，初始化 S = <A>, V = 空集∅ 任取可以和s国贸易的国家c（不属于S和V）置于树的当前生成位置，然后用（S' = <S, c>和V' = V ∪ ∅）生成左子树，用（S' = S和V' = V ∪ {c}）生成右子树。如果c不存在或者s = B则终止当前子树的生成。

• 每个节点保存当前的贸易顺序 S、和已经否决的国家列表 V，初始化根节点为 S=<A>, V = 空集，寻找可以和当前贸易顺序尾部国家直接通商，且不属于 S 和 V 的国家 c，左子树表示贸易顺序上的下一个国家为 c， 用（S' = <S, c>和V' = V ）生成左子树。右子树表示不与 c 进行贸易，用（S' = S和V' = V ∪ {c}）生成右子树。如果c不存在或者s = B则终止当前子树的生成。

• 遍历搜索树的原则：

  • 前进：当前节点未被剪枝，并且仍有子节点
  • 分支：先遍历左分支，再遍历右分支
  • 回溯：找到一个可行解，或当前节点被剪枝，则返回父节点
  • 剪枝：
    • 当前节点贸易税费下界 >= 已求得最优解
    • 当前节点贸易所需时间下界 > t

• 下界：

  • 税费下界和时间下界，可由最短路径算法，构造当前节点到 B 的最短时间 和最短税费路径 + 当前已经确定的税费和时间 得到
  • 正确和有效的原因：下界弱化了限制，在加上任何约束条件的情况下，可行解的花费均大于等于最短路径的费用代价

• 伪代码：

  def Trade(C, R, T, t):
  	# C:国家列表， R 贸易税率矩阵，T:贸易时间矩阵，t:交易最大时间
  	Search(<A>,  ∅)
  	return 最优解
  	
  def Search(S, V):
  	s = S.last
  	if (minTaxBound(S, R) < bestTax && minTimeBound(S, T) <= t)
  		if s == b:
  			记录 S 为当前最优解；更新 bestTax
  		else:
  			寻找可以和 s 进行贸易，且不属于 S，不属于 V 的国家 c：
  				Search(<S,c>, V)
  				Search(<S>, <V,c>)
  		
  

近似算法

• 对每个顶点 $v_i\in V$ 定义变量 $x_i$ 使得，当 $v_i \in C$ 时，$x_i = 1$ 否则，$x_i=0$ 。约束条件：对任意边$(v_i, v_j)$ ，两个顶点至少有一个必须在顶点覆盖 C 中，即$x_i+x_j \ge 1$

• 贪心算法，每一轮更新集合的权重为 wi/(Si - C) ，即集合的权重/加入这个集合后，新增的元素个数，每轮将最小权重的集合加入到 C 中，直到 C 为全集 U

  Chvatal V. A greedy heuristic for the set-covering problem[J]. Mathematics of operations research, 1979, 4(3): 233-235.

贪心算法

设计一针对以下问题的贪心算法，简述算法的基本思想，写出伪代码，并分析其时间复杂性（不一定要找到最优解）：

有n项任务要完成，恰好有n个人可以分别去完成其中一项，但由于任务性质和个人专长不同，因此个人去完成不同的任务的效率（或所费时间）就有差别. 设给定效率矩阵C，矩阵的元素 表示第i人去完成第j项任务所需的时间，则如何分派这n个人去完成这n项任务能使花费的总时间最少。

其他

设计一种策略，使在下面的游戏中，期望提问的平均次数最少（请给出你得到这一策略的过程）：一副纸牌，由一张A，两张2，三张3，直到9张9组成。有人从洗过的这副牌中抽出一张，你需要问一连串用是或否来回答的问题来确定这张牌的点数。

设计一种策略，使在下面的游戏中，期望提问的平均次数最少（请给出你得到这一策略的过程）：

一个黑盒内共有1个红球，2个蓝球，3个绿球，4个黄球，5个黑球，6个白球，7个紫球。有一个人从黑盒内随机拿出一个球，另一个人被蒙上眼睛，只能通过一连串用是或否来回答的问题来确定球的颜色，问该蒙眼人的提问策略。